搜索算法是利用计算机的高性能来有目的的穷举一个问题解空间的部分或所有的可能情况,从而求出问题的解的一种方法。
搜算算法是竞赛中常用的算法。很多题目都可以通过搜索拿部分分,如果有剪枝优化,甚至有可能拿更高的分数。一句话,骗分过样例,暴力出奇迹。
本文将简要介绍常用的DFS和BFS的模型
DFS
深度优先搜索。它的基本思想是:为了求得问题的解,先选择某一种可能情况向前(子结点)探索,在探索过程中,一旦发现原来的选择不符合要求,就回溯至父亲结点重新选择另一结点,继续向前探索,如此反复进行,直至求得最优解。
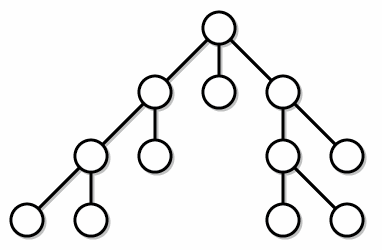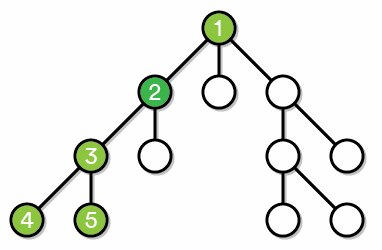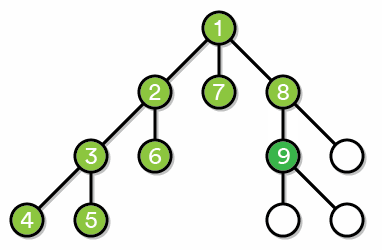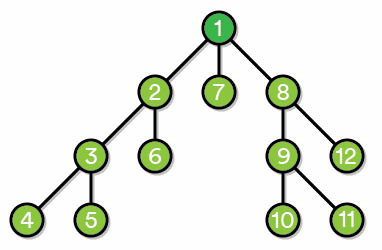
通俗地将,就是不撞南墙不回头,撞了就掉头,一冲到底不服输。
优点:
- 代码量通常较小,框架较为固定,比较容易理解
- 占用空间小,数据量小很快出解
缺点: - 递归调用,容易爆栈
- 数据量大时便利整个解答树速度很慢
- 找到的第一个解并不一定就是最优解
大体框架:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void dfs(int dep){
if(dep==n+1){
//执行输出操作
return;
}
//特殊边界,直接return
for 枚举每个可能的位置或者决策方案{
//可以加入一些剪枝
if(方案合法){
//做标记
dfs(dep+1);
//删标记(回溯)
}
}
}
例题:八皇后问题
检查一个如下的6 x 6的跳棋棋盘,有六个棋子被放置在棋盘上,使得每行、每列有且只有一个,每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。
上面的布局可以用序列2 4 6 1 3 5来描述,第i个数字表示在第i行的相应位置有一个棋子,如下:
行号 1 2 3 4 5 6
列号 2 4 6 1 3 5
这只是跳棋放置的一个解。请编一个程序找出所有跳棋放置的解。并把它们以上面的序列方法输出。解按字典顺序排列。请输出前3个解。最后一行是解的总个数。
输入格式:
一个数字N (6 <= N <= 13) 表示棋盘是N x N大小的。
输出格式:
前三行为前三个解,每个解的两个数字之间用一个空格隔开。第四行只有一个数字,表示解的总数。
输入样例#1:6
输出样例#1:1
2
3
4
5
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
代码1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <cstdio>
using namespace std;
int n,cnt,ans[15];
bool check(int x,int y){//检查是否会出现互吃情况
for(int i=1;i<x;++i){
if(ans[i]==y||x-y==i-ans[i]||x+y==i+ans[i])return false;
}
return true;
}
void dfs(int now){//搜索函数
if(now>n){
++cnt;
if(cnt<=3){
for(int i=1;i<=n;++i)printf("%d ",ans[i]);
printf("\n");
}
return;
}
for(int i=1;i<=n;++i){
if(check(now,i)){//判断是否合理
ans[now]=i;
dfs(now+1);
}
}
}
int main(){
scanf("%d",&n);
if(n==13){//如果n=13会炸
printf("1 3 5 2 9 12 10 13 4 6 8 11 7\n");
printf("1 3 5 7 9 11 13 2 4 6 8 10 12\n");
printf("1 3 5 7 12 10 13 6 4 2 8 11 9\n73712");
return 0;
}
dfs(1);//开始搜索
printf("%d",cnt);
return 0;
}
BFS
广度优先搜索。从根节点出发,找到所有与之相连的第一层节点,依次遍历,遍历的同时找到扩展到的下一层节点,储存起来方便下一步搜索。
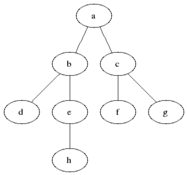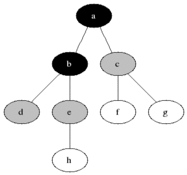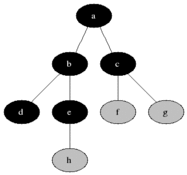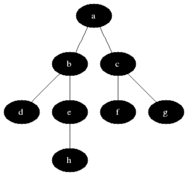
通俗地将,按层搜索,广度优先,队列储存,首解最优。
优点:可以得到最优解,时间效率较高。
缺点:在树的层次较深且子节点个数较多的情况下,消耗内存现象十分严重
大体框架:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void bfs(int s){
queue<int> q;
q.push(s);
vis[s] = true;
while (!q.empty()){
int u = q.front();
q.pop();
for (遍历所有与u相邻的节点){
if (当前找到的扩展节点为解){
执行输出操作
}
if (!vis[u]){
q.push(u);
vis[u] = true;
}
}
}
return ;
}
例题:字串变换
已知有两个字串 A, B 及一组字串变换的规则(至多6个规则):
A1 -> B1
A2 -> B2
规则的含义为:在 A$中的子串 A1 可以变换为 B1、A2 可以变换为 B2 …。
例如:A=’abcd’B=’xyz’
变换规则为:
‘abc’->‘xu’‘ud’->‘y’‘y’->‘yz’
则此时,A 可以经过一系列的变换变为 B,其变换的过程为:
‘abcd’->‘xud’->‘xy’->‘xyz’
共进行了三次变换,使得 A 变换为B
输入格式:
输入格式如下:
A B A1 B1 \
A2 B2 |-> 变换规则
… … /
所有字符串长度的上限为 20。
输出格式:
输出至屏幕。格式如下:
若在 10 步(包含 10步)以内能将 A 变换为 B ,则输出最少的变换步数;否则输出”NO ANSWER!”
输入样例#1:1
2
3
4
5
abcd xyz
abc xu
ud y
y yz
输出样例#1:3
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <iostream>
#include <string>
#include <cstring>
#include <queue>
#include <map>
#define maxn 15
using namespace std;
struct node{
string str;
int step;
};
string a,b;
string orginal[maxn];
string translated[maxn];
int n,ans;
map<string,int> ma;
string trans(const string &str,int i,int j){
string ans = "";
if (i+orginal[j].length() > str.length())
return ans;
for (int k=0; k < orginal[j].length();k++)
if (str[i+k] != orginal[j][k])
return ans;
ans = str.substr(0,i);
ans+=translated[j];
ans+=str.substr(i+orginal[j].length());
return ans;
}
void bfs(){
queue <node> q;
node s;
s.str = a;
s.step = 0;
q.push(s);
while (!q.empty()){
node u = q.front();
q.pop();
string temp;
if(ma.count(u.str) == 1)
continue;
if (u.str == b){
ans = u.step;
break;
}
ma[u.str] = 1;
for (int i=0;i < u.str.length();i++)
for (int j=0; j<n; j++){
temp = trans(u.str,i,j);
if (temp != ""){
node v;
v.str = temp;
v.step = u.step+1;
q.push(v);
}
}
}
if (ans > 10 || ans == 0)
cout << "NO ANSWER!" << endl;
else
cout << ans << endl;
}
int main(){
cin >> a >> b;
while (cin >> orginal[n] >> translated[n])
n++;
bfs();
return 0;
}
总结
还有一些其他的搜索算法,比如迭代加深搜索,启发式搜索等等,今天就不介绍了。
BFS和DFS各有春秋,两者都应该熟练掌握,根据实际情况选择最佳算法。