树状数组

发表于

lowbit

lowbit(n)取出非负整数n在二进制表示下最低位的1及后面的0所构成的数 如lowbit(7)=1 lowbit(6)=2

设lowbit(n)=k

n的第k位是1，后面的k-1位都是0

先将其取反，则第k位变成0，k-1位都变成1

此时n+1,进位 n的k+1位到最高位恰好与原来相反

综上 n & (~n+1)=k

故lowbit(n)=k=n & (~n+1)=n & -n

树状数组

一个正整数x可以二进制分解为

x=2^i1+2^i2+……2^im

设i1>i2>……>im

则区间[1,x]可以分成log x个区间

1 [1,2^i1]

2 [2^i1+1,2^i1+2^i2]

……

m [2^i1+……2^i(m-1)+1,2^i1+……2^im]

这些小区间有一个性质，就是区间长度为结尾数r的lowbit(r)值

树状数组基于上述思想，其用途是维护序列的前缀和。

对于给定序列a，建立一个数组c，其中c[x]表示a区间[x-lowbit(x)+1,x]中所有数的和

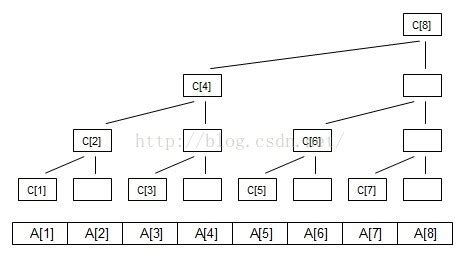
性质

  1. 每个c[x]保存以他为根的子树中所有叶节点的和
  2. 每个c[x]的子节点个数为lowbit(x)
  3. 除数根外，每个c[x]的父节点是c[lowbit(x)+x]
  4. 树的深度为log N

操作

  1. 查询前缀和 即原序列a的1～x个数的和
  2. 若要查询区间[l,r]的和，只需计算ask(r)-ask(l-1)
  3. 单点增加，即给序列中一个数a[x]增加y,同时维护前缀和
  4. 初始化，对每个位置进行add(x,a[x])

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
using namespace std;
int m,n;
int a[500005],c[500005];
int lowbit(int x){
	return (x & -x);
}
void add(int x,int y){
	for(;x<=n;x+=lowbit(x))c[x]+=y;
}
int ask(int x){
	int ans=0;
	for( ;x;x-=lowbit(x))ans+=c[x];
	return ans;
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;++i){
		cin>>a[i];
		add(i,a[i]);
	}
	for(int i=1;i<=m;++i){
		int t,a1,a2;
		cin>>t>>a1>>a2;
		if(t==1)add(a1,a2);
		else cout<<ask(a2)-ask(a1-1)<<endl;
	}
}