栈与单调栈

发表于

栈

栈是一种常见的数据类型，特点是只允许在一端进出，即后进先出原则

基础操作：入栈（push） 出栈 （pop）

一个栈可以定为长n的数组s表示，用一个栈指针top指向栈顶

top=n栈满 top=0栈空

入栈

若top>=n栈溢出 做错误处理

否则，s[++top]=x

出栈

若top<=0 做错误处理

否则，x=s[top],–top

STL

需包含头文件

1
2
3
4
5
6
7
8
9
10
//指定元素 
stack<int>s;
stack<string>s1;
入栈
s.push(x);
出栈(出栈只删除，不返回)
访问栈顶
x=s.top();
判断栈空 s.empty(); 栈空返回true
元素个数 s.size();

例

利用栈结构求后缀表达式

形如“ A B op ” 其中op为运算符 如 ‘’1 2 - 3 ‘’为3(1-2)

建立一个用于存数的栈，对元素逐一扫描

如果遇到一个数，入栈

否则，把栈顶的两个数运算后结果入栈

最终，栈中恰好剩下的数就是结果

单调栈

概念

栈里面的元素的大小按照他们所在栈内的位置，满足一定的单调性。

操作

加入给定一个数组，有若干个元素要加入单调栈且随时维护

若果栈顶的元素是a,要加入栈的元素为b

若a大于b 符合单调栈的单调递增性质 入栈 栈顶变为a

若a小于b 不符合要求，在a前面至少有一个（b）元素使其不能拓展

故只有当a找到自己的位置时候才能入栈 否则不能入栈

性质

栈内元素呈单调性

元素加入栈前，会在栈顶端把破坏栈单调性的元素都删除

使用单调栈可以找到元素向左遍历第一个比他小的元素，也可以找到元素向左遍历第一个比他大的元素。

典例

原题地址POJ2559

img

如图，有若干个矩形，求包含于这些矩形的并集内部的最大矩形的面积 上图的答案就是阴影面积 矩形个数<=10^5

分析

如果高度自左而右单调递增，那么我们可以尝试以每个矩形的高度作为答案的高度一一枚举并把宽度延伸至右边界，得到一个值，其中最大的就是最终答案

但是 如果下一个矩形的高度比上一个小

显然该矩形如果利用之前的矩形一起构成一块较大的面积时，这块面积的高度就不可能超过该矩形自己的高度了

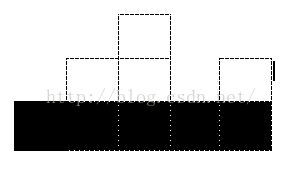
上图中的白色部分可以被删除了

我们不妨用一个宽度累加，高度为该矩形自己的高度的新矩形，即黑色部分代替

于是我们维护的便是一个递增的矩阵序列，即单调栈

  1. 建立一个栈，保存若干个矩形
  2. 从左而又依次扫描，如果当前矩形比栈顶的高 直接入栈
  3. 否则不断取出栈顶，直至栈为空或者栈顶矩形的高度比当前的小
  4. 在3的出栈过程中，累积被弹出的矩形宽度之和，并且每弹一个，就用它的高度乘累积宽度更新答案。整个出栈过程结束后，我们把一个高度为当前高度，宽度为累计值的新矩形入栈
  5. 整个扫描结束后，把栈中剩余矩形依次弹出，按照上述方法更新答案 为了防止栈中还有剩余元素，可以新建一个高度为0的矩形a[n+1]

关键代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
a[n+1]=p=0;
for(int i=1;i<=n+1;++i){
    if(a[i]>s[p]){
        s[++p]=a[i];
        w[p]=1;
    }
    else{
        int width=0;
        while(s[p]>a[i]){
            width+=w[p];
            ans=max(ans,(long long)width*s[p]);
            p--;
        }
        s[++p]=a[i],w[p]=width+1;
    }
}