AES算法

发表于

AES简介

AES加密算法即密码学中的高级加密标准（Advanced Encryption Standard，AES），又称Rijndael加密法，是美国联邦政府采用的一种区块加密标准。这个标准用来替代原先的DES，已经被多方分析且广为全世界所使用。经过五年的甄选流程，高级加密标准由美国国家标准与技术研究院 （NIST）于2001年11月26日发布于FIPS PUB 197，并在2002年5月26日成为有效的标准。

AES算法本质上是一种对称分组密码体制，采用代替/置换网络，每轮由三层组成：线性混合层确保多轮之上的高度扩散，非线性层由16个S盒并置起到混淆的作用，密钥加密层将子密钥异或到中间状态。AES是一个迭代分组密码，其分组长度和密钥长度都是可变的，只是为了满足AES的要求才限定处理的分组大小为128位，而密钥长度为128位、192位或256位，相应的迭代轮数N，为10轮、12轮、14轮。AES汇聚了安全性能、效率、可实现性、灵活性等优点。最大的优点是可以给出算法的最佳查分特征的概率，并分析算法抵抗查分密码分析及线性密码分析的能力。

AES算法概述

AES算法，基本变换包括SubBytes（字节替代）、ShiftRows（行移位）、MixColumns（列混淆）、AddRoundKey(轮密钥加）KeyExtension（密钥扩展）

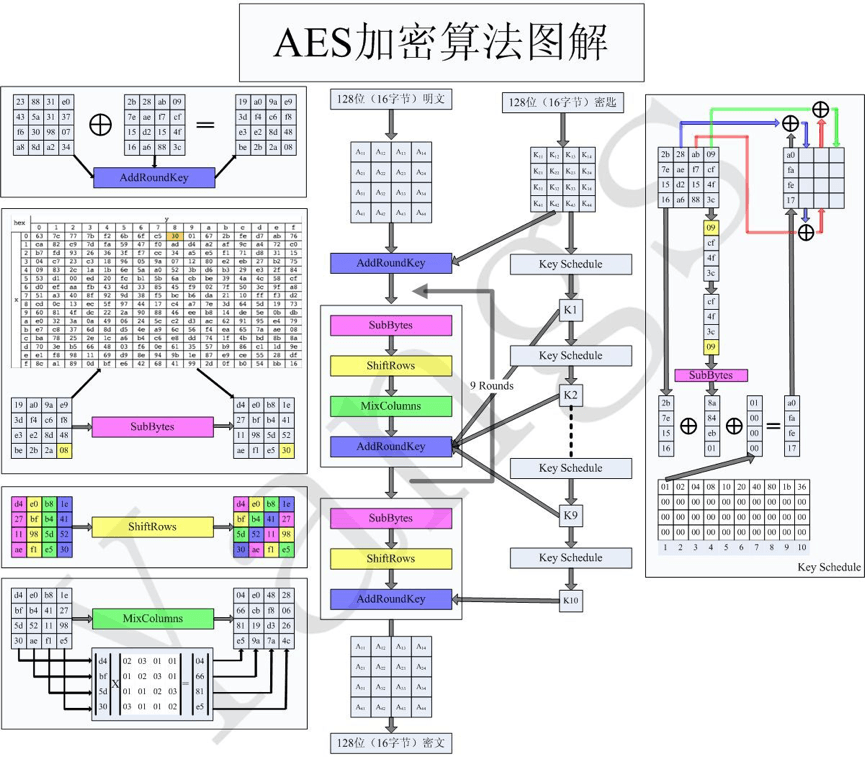
AES算法中的加密、解密过程要经过多次数据变换操作，每一次变换操作会产生一个中间结果，称为状态(State)，算法的执行过程如下：

①：给定一个明文M，将State初始化为M，并进行AddRoundKey操作，将轮密钥与State异或。

②：对前Nr-1轮中的每一轮，用S盒进行一次SubBytes代替变换，对State做一次ShiftRows行移位操作，再对State做一次MixColumns列混淆操作，然后进行AddRoundKey操作。

③：按照顺序分别进行SubBytes、ShiftRows、AddRoundKey操作。

④：将最后的State中的内容定义为密文C。

AES的解密算法于加密不同，基本运算中除轮密钥加(AddRoundKey)不变之外，其余操作如SubBytes、ShiftRows、MixColumns都要求进行求逆变换。

AES算法详解

明文及密钥的组织排列方式(以明文分组为128bits为例组成的阵列)：

以明文分组（或密钥）为128bits、192bits 、256bits为例组成的阵列：

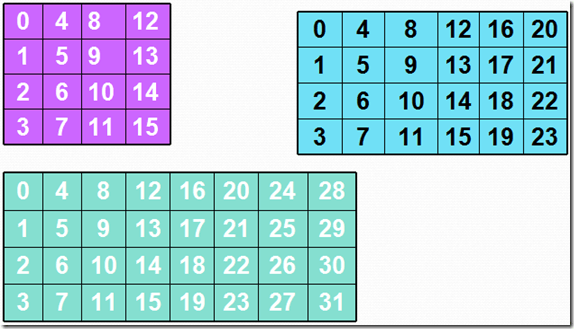
一些相关的的术语定义和表示：

  • 状态（State）：密码运算的中间结果称为状态。
  • State的表示：状态用以字节为基本构成元素的矩阵阵列来表示，该阵列有4行，列数记为Nb。 Nb=分组长度（bits）÷ 32 Nb可以取的值为4，6，8，对应的分组长度为128， 192， 256 bits。
  • 密码密钥（Cipher Key）的表示： Cipher Key类似地用一个4行的矩阵阵列来表示，列数记为Nk。 Nk=密钥长度（bits）÷32 Nk可以取的值为4，6，8，对应的密钥长度为128， 192， 256 bits。

轮数（Round）的不同取值：

ByteSubstitution(字节替代)

非线性的字节替代，单独处理每个字节：

求该字节在有限域GF(2^8)上的乘法逆，”0”被映射为自身，即对于α∈GF(2^8)，求β∈GF(2^8)，

使得 α·β=β·α=1mod(x^8+x^4+x^2+x+1)。

对上一步求得的乘法逆作仿射变换

yi=xi + x(i+4)mod8 + x(i+6)mod8 + x(i+7)mod8 + ci

(其中ci是6310即011000112的第i位），用矩阵表示为：

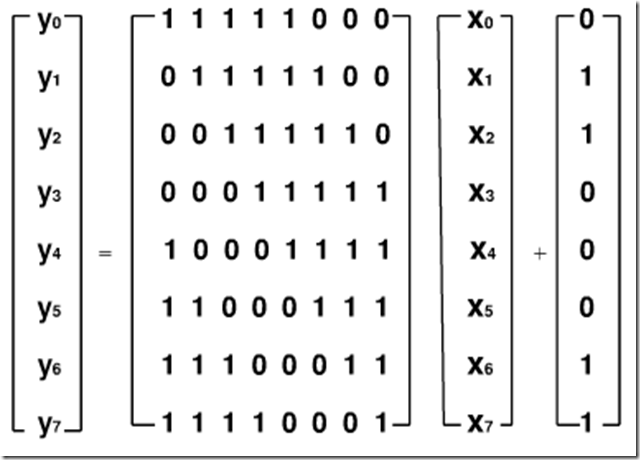
下面直接利用置换表完成替换：

1
2
3
4
5
6
7
8
9
10
11
void AES::SubBytes(unsigned char state[][4])
{
    int r,c;
    for(r=0; r<4; r++)
    {
        for(c=0; c<4; c++)
        {
            state[r][c] = Sbox[state[r][c]];
        }
    }
}

ShiftRows(行移位变换)

行移位变换完成基于行的循环位移操作，变换方法：

在ByteRotation变换中，状态阵列的后3行循环移位不同的偏移量。移位变换作用于行上，第0行不变，第1行循环移位C1字节，第2行循环移位C2字节，第3行循环移位C3字节。

偏移量C1、C2、C3与分组长度Nb有关，如下表所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
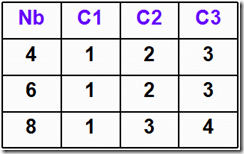
16
void AES::ShiftRows(unsigned char state[][4])
{
    unsigned char t[4];
    int r,c;
    for(r=1; r<4; r++)
    {
        for(c=0; c<4; c++)
        {
            t[c] = state[r][(c+r)%4];
        }
        for(c=0; c<4; c++)
        {
            state[r][c] = t[c];
        }
    }
}

MixColumns(列混淆变换)

将状态的列看作是有限域GF(2^8)上的多项式a(x)，与多项式c(x)=(03·x^3 + 01·x^2 + 01·x + 02) · mod(x^4 + 1)。

逐列混合，方法：

b(x) = (03·x^3 + 01·x^2 + 01·x + 02) · a(x) mod(x^4 + 1)

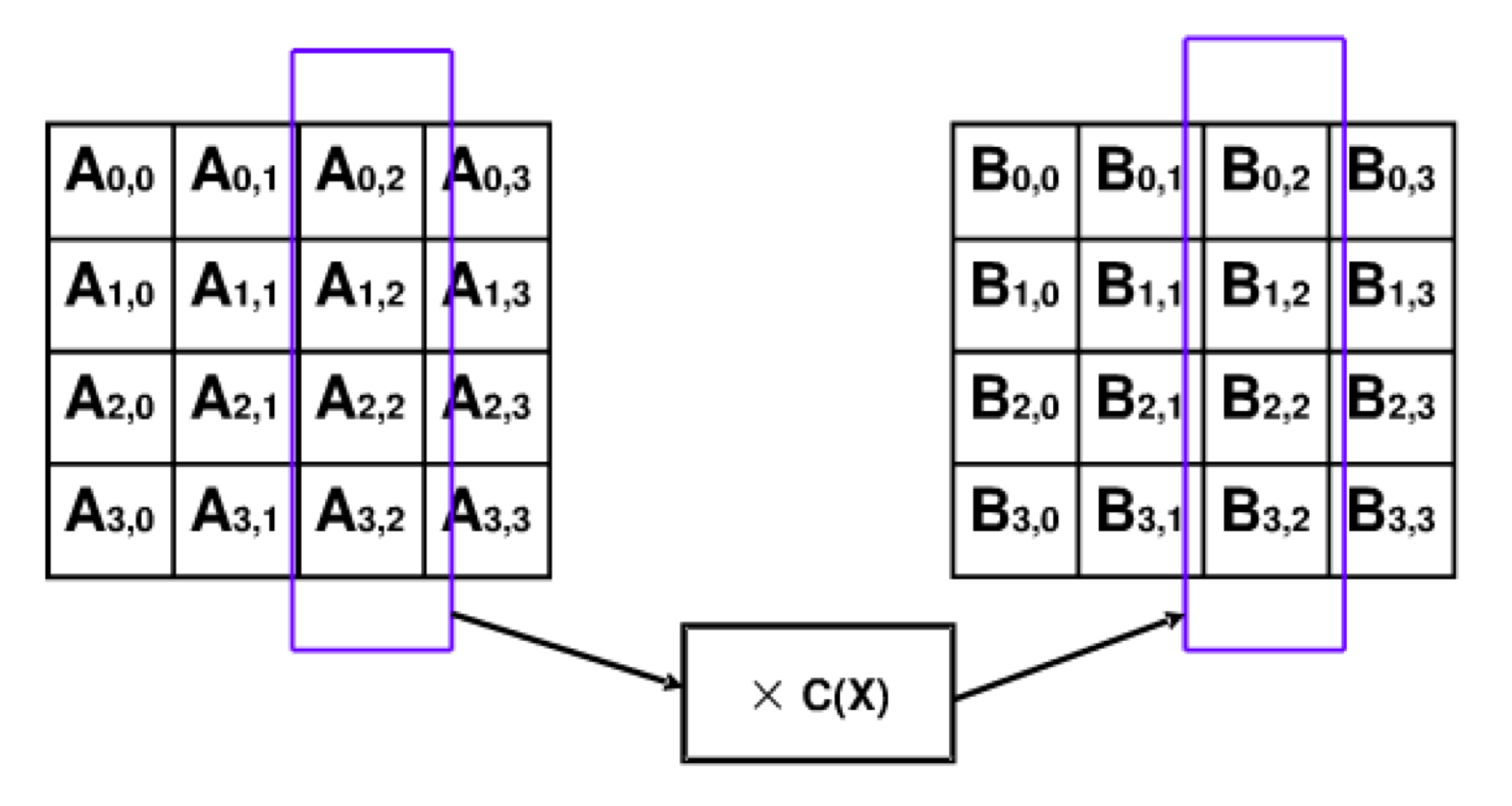
矩阵表示形式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
void AES::MixColumns(unsigned char state[][4])
{
    unsigned char t[4];
    int r,c;
    for(c=0; c< 4; c++)
    {
        for(r=0; r<4; r++)
        {
            t[r] = state[r][c];
        }
        for(r=0; r<4; r++)
        {
            state[r][c] = FFmul(0x02, t[r])
                        ^ FFmul(0x03, t[(r+1)%4])
                        ^ FFmul(0x01, t[(r+2)%4])
                        ^ FFmul(0x01, t[(r+3)%4]);
        }
    }
}
 
unsigned char AES::FFmul(unsigned char a, unsigned char b)
{
    unsigned char bw[4];
    unsigned char res=0;
    int i;
    bw[0] = b;
    for(i=1; i<4; i++)
    {
        bw[i] = bw[i-1]<<1;
        if(bw[i-1]&0x80)
        {
            bw[i]^=0x1b;
        }
    }
    for(i=0; i<4; i++)
    {
        if((a>>i)&0x01)
        {
            res ^= bw[i];
        }
    }
    return res;
}

其中FFmul为有限域GF(28)上的乘法，标准算法应该是循环8次（b与a的每一位相乘，结果相加），但这里只用到最低2位，解密时用到的逆列混淆也只用了低4位，所以在这里高4位的运算是多余的，只计算低4位。

数学基础

AES的基础域是有限域 GF(2^8)：
一个GF(2)上的8次既约多项式可生成一个 GF(2^8)
GF(2^8)的全体元素构成加法交换群，线性空间。
GF(2^8)的非零元素构成乘法循环群。
GF(2^8)中的元素有多种表示：
字节： GF（2^8）={a7,a6,…a1,a0}
多项式形式： GF（2^8）={a7x7+a6x6+…+a1x+a0}
指数形式：GF(2^8)={0, 1… 254}对数形式：GF(2^8)={0, 1… 254}

GF(2^8)的特征为 2 。

AES的GF(2^8)表示：
AES采用的既约模多项式：
m(x)=x^8+x^4+x^3+x+1
AES采用GF(28)的多项式元素表示。
字节B＝b7b6b5b4b3b2b1b0可表示成GF(2)上的多项式：
b7x7+b6x6+b5x5+b4x4+b3x3+b2x2+b1x1+b0
例：字节57＝01010111的多项式表示：
01010111 x^6+x^4+x^2+x+1

加法：两元素多项式的系数按位模 2加
例2：57＋83＝D4
(x6+x4+x2+x+1)⊕(x7+x+1)= x7+x6+x4+x2
乘法：两元素多项式相乘，模 m(x)
例3：57×83＝C1
(x6+x4+x2+x+1)×(x7+x+1)=x7+x6+1 mod m(x)
乘法单位元：字节01 多项式 1
乘法逆元：
设a(x)的逆元为b(x)，则 a(x)b(x)=1 mod m(x) 。
根据Euclid算法求出。

AddRoundKey(轮密钥加变换)

简单来说就是逐字节相加，有限域GF(2^8)上的加法是模2加法，即异或：

1
2
3
4
5
6
7
8
9
10
11
void AES::AddRoundKey(unsigned char state[][4], unsigned char k[][4])
{
    int r,c;
    for(c=0; c<4; c++)
    {
        for(r=0; r<4; r++)
        {
            state[r][c] ^= k[r][c];
        }
    }
}

KeyExpansion(密钥扩展)

密钥bit的总数＝分组长度×（轮数Round＋1）例如当分组长度为128bits和轮数Round为10时，轮密钥长度为128×(10＋1)＝1408bits。
将密码密钥扩展成一个扩展密钥。
从扩展密钥中取出轮密钥：第一个轮密钥由扩展密钥的第一个Nb个4字节字，第二个轮密钥由接下来的Nb个4字节字组成，以此类推。

将输入的密钥扩展为11组128位密钥组，其中第0组为输入密钥本身

其后第n组第i列 为 第n-1组第i列 与 第n组第i-1列之和（模2加法，1<= i <=3）

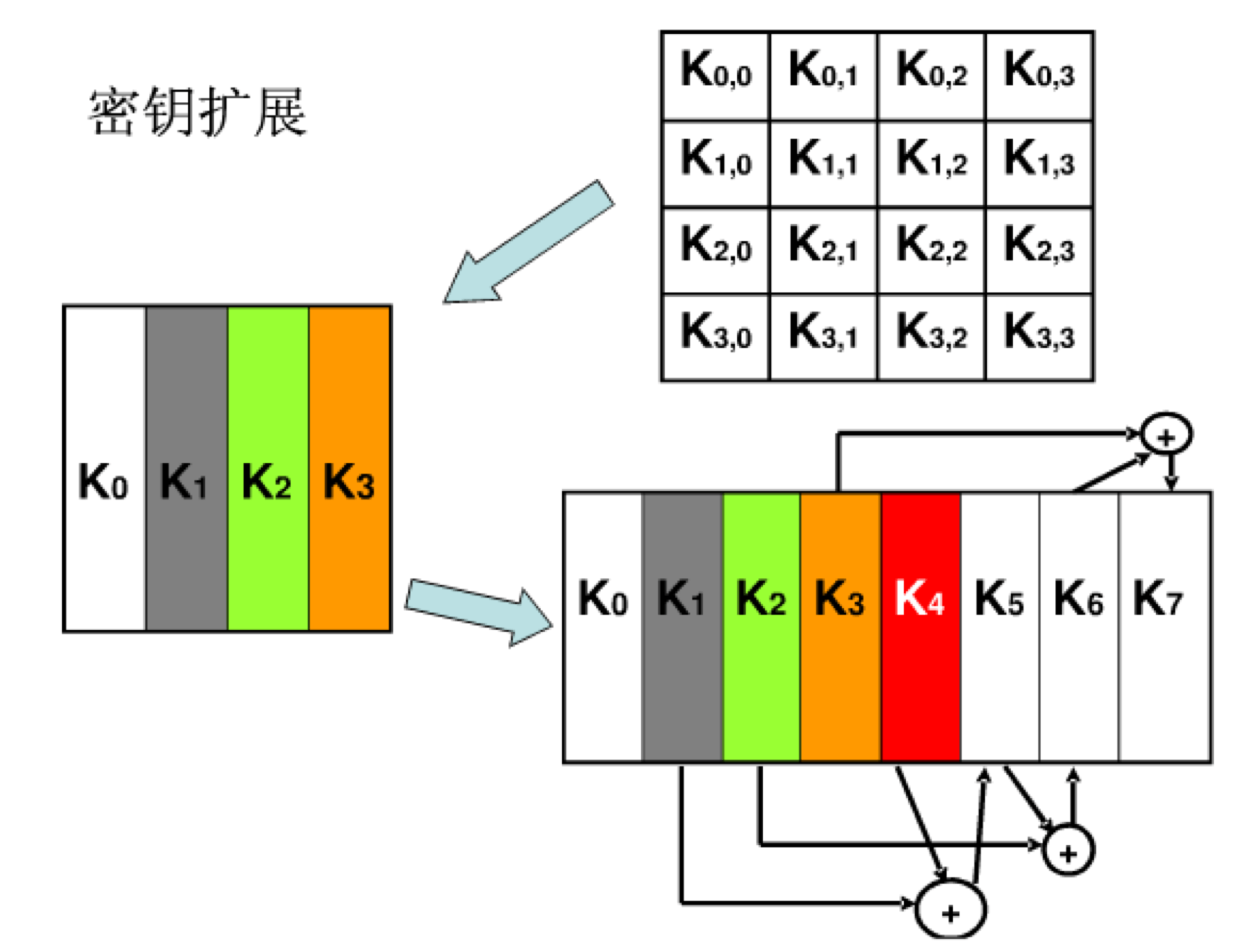
对于每一组 第一列即i=0，有特殊的处理：

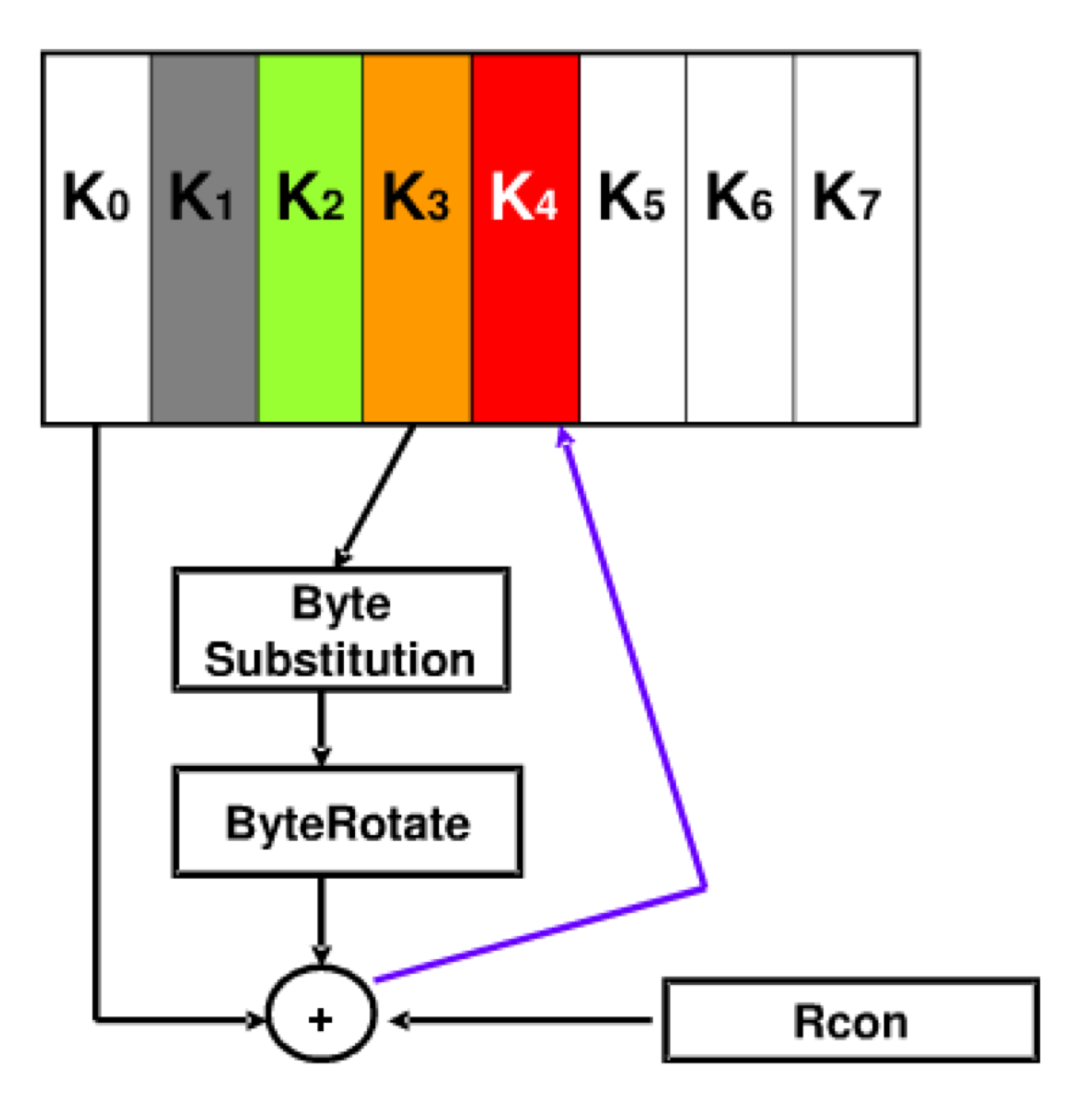
将前一列即第n-1组第3列的4个字节循环左移1个字节，
并对每个字节进行字节替代变换SubBytes
将第一行（即第一个字节）与轮常量rc[n]相加
最后再与前一组该列相加。

加密过程

先将输入的明文按列序组合成4*4的矩阵，直接与第0组密钥（即输入的密钥）相加（异或），作为轮加密的输入。

然后循环10次进行SubBytes、ShiftRows、MixColumns、AddRoundKey运算，最后恢复原序列。

需要注意的是最后一轮并不进行MixColumns（列混淆变换）

解密的基本运算

AES解密算法与加密不同，基本运算中除了AddRoundKey（轮密钥加）不变外，其余的都需要进行逆变换，即

InvSubBytes（逆字节替代）、InvShiftRows（逆行移位）、InvMixColumns（逆列混淆）。