模拟退火算法

历史背景

美国物理学家 N.Metropolis 和同仁在1953年发表研究复杂系统、计算其中能量分布的文章，他们使用蒙特卡罗模拟法计算多分子系统中分子的能量分布。这相当于是本文所探讨之问题的开始，事实上，模拟退火中常常被提到的一个名词就是Metropolis准则 。

美国IBM公司物理学家 S.Kirkpatrick、C. D. Gelatt 和 M. P. Vecchi 于1983年在《Science》上发表了一篇颇具影响力的文章：《以模拟退火法进行最优化（Optimization by Simulated Annealing）》。他们借用了Metropolis等人的方法探讨一种旋转玻璃态系统（spin glass system）时，发觉其物理系统的能量和一些组合最优（combinatorial optimization）问题（著名的旅行推销员问题TSP即是一个代表例子）的成本函数相当类似：寻求最低成本即似寻求最低能量。由此，他们发展出以 Metropolis 方法为本的一套算法，并用其来解决组合问题等的寻求最优解。

几乎同时，欧洲物理学家 V.Carny 也发表了几乎相同的成果，但两者是各自独立发现的；只是Carny“运气不佳”，当时没什么人注意到他的大作；或许可以说，《Science》杂志行销全球，“曝光度”很高，素负盛名，而Carny却在另外一本发行量很小的专门学术期刊《J.Opt.Theory Appl.》发表其成果因而并未引起应有的关注。

Kirkpatrick等人受到Metropolis等人用蒙特卡罗模拟的启发而发明了“模拟退火”这个名词，因为它和物体退火过程相类似。寻找问题的最优解（最值）即类似寻找系统的最低能量。因此系统降温时，能量也逐渐下降，而同样意义地，问题的解也“下降”到最值。

物理背景

在热力学上，退火（annealing）现象指物体逐渐降温的物理现象，温度愈低，物体的能量状态会低；够低后，液体开始冷凝与结晶，在结晶状态时，系统的能量状态最低。大自然在缓慢降温（亦即，退火）时，可“找到”最低能量状态：结晶。但是，如果过程过急过快，快速降温（亦称「淬炼」，quenching）时，会导致不是最低能态的非晶形。

如下图所示，首先物体处于非晶体状态。我们将固体加温至充分高，再让其徐徐冷却，也就退火。加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小（此时物体以晶体形态呈现）。

算法内容

想象一下如果我们现在有下面这样一个函数，现在想求函数的（全局）最优解。如果采用Greedy策略，那么从A点开始试探，如果函数值继续减少，那么试探过程就会继续。而当到达点B时，显然我们的探求过程就结束了（因为无论朝哪个方向努力，结果只会越来越大）。最终我们只能找打一个局部最后解B。

模拟退火其实也是一种Greedy算法，但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。以上图为例，模拟退火算法在搜索到局部最优解B后，会以一定的概率接受向右继续移动。也许经过几次这样的不是局部最优的移动后会到达B 和C之间的峰点，于是就跳出了局部最小值B。

根据Metropolis准则，粒子在温度T时趋于平衡的概率为exp(-ΔE/(kT))，其中E为温度T时的内能，ΔE为其改变数,k为Boltzmann常数。Metropolis准则常表示为

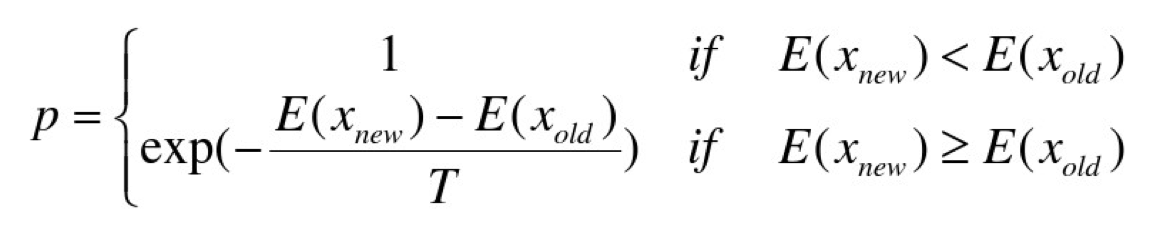
Metropolis准则表明，在温度为T时，出现能量差为dE的降温的概率为P(dE)，表示为：P(dE) = exp( dE/(kT) )。其中k是一个常数，exp表示自然指数，且dE<0。所以P和T正相关。这条公式就表示：温度越高，出现一次能量差为dE的降温的概率就越大；温度越低，则出现降温的概率就越小。又由于dE总是小于0（因为退火的过程是温度逐渐下降的过程），因此dE/kT < 0 ，所以P(dE)的函数取值范围是(0,1) 。随着温度T的降低，P(dE)会逐渐降低。

我们将一次向较差解的移动看做一次温度跳变过程，我们以概率P(dE)来接受这样的移动。也就是说，在用固体退火模拟组合优化问题，将内能E模拟为目标函数值 f，温度T演化成控制参数 t，即得到解组合优化问题的模拟退火演算法：由初始解 i 和控制参数初值 t 开始，对当前解重复“产生新解→计算目标函数差→接受或丢弃”的迭代，并逐步衰减 t 值，算法终止时的当前解即为所得近似最优解，这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制，包括控制参数的初值 t 及其衰减因子Δt 、每个 t 值时的迭代次数L和停止条件S。

总结起来就是：

• 若f( Y(i+1) ) <= f( Y(i) ) (即移动后得到更优解)，则总是接受该移动；
• 若f( Y(i+1) ) > f( Y(i) ) (即移动后的解比当前解要差)，则以一定的概率接受移动，而且这个概率随着时间推移逐渐降低（逐渐降低才能趋向稳定）相当于上图中，从B移向BC之间的小波峰时，每次右移（即接受一个更糟糕值）的概率在逐渐降低。如果这个坡特别长，那么很有可能最终我们并不会翻过这个坡。如果它不太长，这很有可能会翻过它，这取决于衰减 t 值的设定。

关于普通Greedy算法与模拟退火，有一个有趣的比喻：

• • 普通Greedy算法：兔子朝着比现在低的地方跳去。它找到了不远处的最低的山谷。但是这座山谷不一定最低的。这就是普通Greedy算法，它不能保证局部最优值就是全局最优值。
  • 模拟退火：兔子喝醉了。它随机地跳了很长时间。这期间，它可能走向低处，也可能踏入平地。但是，它渐渐清醒了并朝最低的方向跳去。这就是模拟退火。

​

​ 通过一个实例来编程演示模拟退火的执行。特别地，我们这里所采用的实例是著名的“旅行商问题”（TSP，Traveling Salesman Problem），它是哈密尔顿回路的一个实例化问题，也是最早被提出的NP问题之一。

费马点问题

题目

题意：给n个点，找出一个点，使这个点到其他所有点的距离之和最小，也就是求费马点。

#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <stdio.h>
#include <time.h>
#include <math.h>
 
#define N 1005
#define eps 1e-8     //搜索停止条件阀值
#define INF 1e99     
#define delta 0.98   //温度下降速度
#define T 100        //初始温度
 
using namespace std;
 
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};  //上下左右四个方向
 
struct Point
{
	double x, y;
};
 
Point p[N];
 
double dist(Point A, Point B)
{
	return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}
 
double GetSum(Point p[], int n, Point t)
{
	double ans = 0;
	while(n--)
		ans += dist(p[n], t);
	return ans;
}
 
//其实我觉得这玩意儿根本不叫模拟退火
double Search(Point p[], int n)
{
	Point s = p[0];    //随机初始化一个点开始搜索
	double t = T;      //初始化温度
	double ans = INF;  //初始答案值
	while(t > eps)
	{
		bool flag = 1;
		while(flag)
		{
			flag = 0;
		    for(int i = 0; i < 4; i++)    //上下左右四个方向
		    {
			    Point z;
			    z.x = s.x + dx[i] * t;
			    z.y = s.y + dy[i] * t;
			    double tp = GetSum(p, n, z);
		        if(ans > tp)
				{
					ans = tp;
					s = z;
					flag = 1;
				}
		    }
		}
		t *= delta;
	}
	return ans;
}
 
int main()
{
	int n;
	while(scanf("%d", &n) != EOF)
	{
		for(int i = 0; i < n; i++)
			scanf("%lf %lf", &p[i].x, &p[i].y);
		printf("%.0lf\n", Search(p, n));
	}
	return 0;
}

题目：平面上给定n条线段，找出一个点，使这个点到这n条线段的距离和最小。

#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <stdio.h>
#include <time.h>
#include <math.h>
 
#define N 1005
#define eps 1e-8     //搜索停止条件阀值
#define INF 1e99     
#define delta 0.98   //温度下降速度
#define T 100        //初始温度
 
using namespace std;
 
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};  //上下左右四个方向
 
struct Point
{
	double x, y;
};
 
Point s[N], t[N];
 
double cross(Point A, Point B, Point C)  
{  
	return (B.x - A.x) * (C.y - A.y) - (B.y - A.y) * (C.x - A.x);  
}  
 
double multi(Point A, Point B, Point C)  
{  
	return (B.x - A.x) * (C.x - A.x) + (B.y - A.y) * (C.y - A.y);  
}  
 
double dist(Point A, Point B)
{
	return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}
 
double GetDist(Point A, Point B, Point C)  
{  
	if(dist(A, B) < eps) return dist(B, C);  
	if(multi(A, B, C) < -eps) return dist(A, C);  
	if(multi(B, A, C) < -eps) return dist(B, C);  
	return fabs(cross(A, B, C) / dist(A, B));  
}  
 
double GetSum(Point s[], Point t[], int n, Point o)
{
	double ans = 0;
	while(n--)
		ans += GetDist(s[n], t[n], o);
	return ans;
}
 
double Search(Point s[], Point t[], int n, Point &o)
{
	o = s[0];    
	double tem = T;      
	double ans = INF;
	while(tem > eps)
	{
		bool flag = 1;
		while(flag)
		{
			flag = 0;
		    for(int i = 0; i < 4; i++)    //上下左右四个方向
		    {
			    Point z;
			    z.x = o.x + dx[i] * tem;
			    z.y = o.y + dy[i] * tem;
			    double tp = GetSum(s, t, n, z);
		        if(ans > tp)
				{
					ans = tp;
					o = z;
					flag = 1;
				}
		    }
		}
		tem *= delta;
	}
	return ans;
}
 
int main()
{
	int n;
	while(scanf("%d", &n) != EOF)
	{
		for(int i = 0; i < n; i++)
			scanf("%lf %lf %lf %lf", &s[i].x, &s[i].y, &t[i].x, &t[i].y);
		Point o;
		double ans = Search(s, t, n, o);
		printf("%.1lf %.1lf %.1lf\n", o.x, o.y, ans);  
	}
	return 0;
}

最小包含球问题

题目

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <math.h>
 
#define N 55
#define eps 1e-7
#define T 100
#define delta 0.98
#define INF 1e99
 
using namespace std;
 
struct Point
{
	double x, y, z;
};
 
Point p[N];
 
double dist(Point A, Point B)
{
	return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y) + (A.z - B.z) * (A.z - B.z));
}
 
double Search(Point p[], int n)
{
	Point s = p[0];
	double t = T;
	double ans = INF;
	while(t > eps)
	{
		int k = 0;
		for(int i = 0; i < n; i++)
			if(dist(s, p[i]) > dist(s, p[k]))
				k = i;
		double d = dist(s, p[k]);
		ans = min(ans, d);
		s.x += (p[k].x - s.x) / d * t;
		s.y += (p[k].y - s.y) / d * t;
		s.z += (p[k].z - s.z) / d * t;
		t *= delta;
	}
    return ans;
}
 
int main()
{
	int n;
    while(cin >> n && n)
	{
		for(int i = 0; i < n; i++)
			cin >> p[i].x >> p[i].y >> p[i].z;
		double ans = Search(p, n);
		printf("%.5lf\n", ans);
	}
	return 0;
}

函数最值问题

题目

给出方程F(x) = 6 x^7+8x^6+7x^3+5x^2-y*x (0 <= x <=100)

输入y 求x的最小值

#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <algorithm>
#include <stdio.h>
#include <time.h>
#include <math.h>
 
#define ITERS 10
#define T 100
#define eps 1e-8
#define delta 0.98
#define INF 1e99
 
using namespace std;
 
double x[ITERS];
 
int Judge(double x, double y)
{
	if(fabs(x - y) < eps) return 0;
	return x < y ? -1 : 1;
}
 
double Random()
{
	double x = rand() * 1.0 / RAND_MAX;
	if(rand() & 1) x *= -1;
	return x;
}
 
double F(double x, double y)
{
	return 6 * x * x * x * x * x * x * x + 8 * x * x * x * x * x * x + 7 * x * x * x + 5 * x * x - y * x;
}
 
void Init()
{
	for(int i = 0; i < ITERS; i++)
		x[i] = fabs(Random()) * 100;
}
 
double SA(double y)
{
	double ans = INF;
	double t = T;
	while(t > eps)
	{
		for(int i = 0; i < ITERS; i++)
		{
			double tmp = F(x[i], y);
			for(int j = 0; j < ITERS; j++)
			{
				double _x = x[i] + Random() * t;
				if(Judge(_x, 0) >= 0 && Judge(_x, 100) <= 0)
				{
					double f = F(_x, y);
					if(tmp > f) 
					    x[i] = _x;
				}
			} 
		}
		t *= delta;
	}
	for(int i = 0; i < ITERS; i++)
		ans = min(ans, F(x[i], y));
	return ans;
}
 
int main()
{
    int t;
	scanf("%d", &t);
	while(t--)
	{
		double y;
		scanf("%lf", &y);
		srand(time(NULL));
		Init();
		printf("%.4lf\n", SA(y));
	}
	return 0;
}

TSP问题

假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。

#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <algorithm>
#include <stdio.h>
#include <time.h>
#include <math.h>
 
#define N     30      //城市数量
#define T     3000    //初始温度
#define EPS   1e-8    //终止温度
#define DELTA 0.98    //温度衰减率
#define LIMIT 10000   //概率选择上限
#define OLOOP 1000    //外循环次数
#define ILOOP 15000   //内循环次数
 
using namespace std;
 
//定义路线结构体
struct Path
{
	int citys[N];
	double len;
};
 
//定义城市点坐标
struct Point
{
	double x, y;
};
 
Path path;        //记录最优路径
Point p[N];       //每个城市的坐标
double w[N][N];   //两两城市之间路径长度
int nCase;        //测试次数
 
double dist(Point A, Point B)
{
	return sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));
}
 
void GetDist(Point p[], int n)
{
	for(int i = 0; i < n; i++)
		for(int j = i + 1; j < n; j++)
			w[i][j] = w[j][i] = dist(p[i], p[j]);
}
 
void Input(Point p[], int &n)
{
	scanf("%d", &n);
	for(int i = 0; i < n; i++)
		scanf("%lf %lf", &p[i].x, &p[i].y);
}
 
void Init(int n)
{
	nCase = 0;
	path.len = 0;
	for(int i = 0; i < n; i++)
	{
		path.citys[i] = i;
		if(i != n - 1)
		{
			printf("%d--->", i);
			path.len += w[i][i + 1];
		}
		else
			printf("%d\n", i);
	}
	printf("\nInit path length is : %.3lf\n", path.len);
}
 
void Print(Path t, int n)
{
	printf("Path is : ");
	for(int i = 0; i < n; i++)
	{
		if(i != n - 1)
			printf("%d-->", t.citys[i]);
		else 
			printf("%d\n", t.citys[i]);
	}
	printf("\nThe path length is : %.3lf\n", t.len);
}
 
Path GetNext(Path p, int n)
{
	Path ans = p;
    int x = (int)(n * (rand() / (RAND_MAX + 1.0)));
	int y = (int)(n * (rand() / (RAND_MAX + 1.0)));
	while(x == y)
	{
		x = (int)(n * (rand() / (RAND_MAX + 1.0)));
		y = (int)(n * (rand() / (RAND_MAX + 1.0)));
	}
	swap(ans.citys[x], ans.citys[y]);
    ans.len = 0;
	for(int i = 0; i < n - 1; i++)
		ans.len += w[ans.citys[i]][ans.citys[i + 1]];
	cout << "nCase = " << nCase << endl;
	Print(ans, n);
	nCase++;
	return ans;
}
 
void SA(int n)
{
	double t = T;
	srand(time(NULL));
	Path curPath = path;
	Path newPath = path;
	int P_L = 0;
	int P_F = 0;
	while(1)       //外循环，主要更新参数t，模拟退火过程
	{
		for(int i = 0; i < ILOOP; i++)    //内循环，寻找在一定温度下的最优值
		{
			newPath = GetNext(curPath, n);
			double dE = newPath.len - curPath.len;
			if(dE < 0)   //如果找到更优值，直接更新
			{
				curPath = newPath;
				P_L = 0;
				P_F = 0;
			}
			else
			{
				double rd = rand() / (RAND_MAX + 1.0);    
				if(exp(dE / t) > rd && exp(dE / t) < 1)   //如果找到比当前更差的解，以一定概率接受该解，并且这个概率会越来越小
					curPath = newPath;
				P_L++;
			}
			if(P_L > LIMIT)
			{
				P_F++;
				break;
			}
		}
		if(curPath.len < newPath.len)
			path = curPath;
		if(P_F > OLOOP || t < EPS)
			break;
		t *= DELTA;
	}
}
 
int main()
{
	freopen("TSP.data", "r", stdin);
	int n;
	Input(p, n);
	GetDist(p, n);
	Init(n);
	SA(n);
	Print(path, n);
    printf("Total test times is : %d\n", nCase);
	return 0;
}

数据

27
41 94
37 84
53 67
25 62
7  64
2  99
68 58
71 44
54 62
83 69
64 60
18 54
22 60
83 46
91 38
25 38
24 42
58 69
71 71
74 78
87 76
18 40
13 40
82  7
62 32
58 35
45 21